Methodology & Application
Bubble 3D is an advanced program to replace your Excel spreadsheets; This program is not a sophisticated finite element or finite difference software! It is critical for the user to understand the assumptions, weak points and limitations of this program.
The way Bubble 3D works, it discretizes the model (defined by dimensions B x L x H) into small soil elements. When a foundation load is applied at the ground surface, Bubble 3D conducts the following analyses:
- The program divides each load area (i.e. foundation load, surcharge, etc) into small triangles (i.e. Cells). The equivalent point load is calculated at the centriod of each triangle.
- The model is divided into soil elements. Each soil element is a cube of Δx * Δy * ΔZ defined by the user.
- The program goes through each soil element; The δP resulted from each load Cell is calculated at the center of the soil elements. Please note there are several load cells for which δP will be calculated at the center of this soil element.
- At each soil element ΔP is calculated by summation of all δP resulted from all load Cells.
- Now the program knows ΔP at the center the all soil elements. At the next step, Bubble 3D calculates elastic and consolidation settlement for all soil elements.
Once the analyses is completed, the program provides a graphical representation for settlement, stress increase, etc.
Elastic Settlement Analysis
The program covers the following methods:
Half-Space Elastic Settlement: using the following equation:
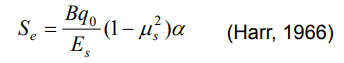
where:
Se: elastic settlement of the soil element,
B: width of the soil element, i.e. the lesser of ΔX or ΔY,
qo: the stress increase ΔP at this soil element,
μs: Poisson's ratio of the soil,
α: function of shape and flexibility of foundation. Bubble 3D uses α = 0.85 for flexible foundation and α = 0.88 for rigid foundation.
Fully Elastic Settlement: This method assumes that soil elements comprise of perfectly elastic material. The following equation is used:
δL=P.L / (AxE)
where:
δL: compression (settlement) of the soil element in Z direction,
P: stress increase, converted to load, at the center of the soil element (i.e. P = ΔP * ΔX * ΔY),
L: length of the soil element in direction of the load (i.e. L = ΔZ),
A: cross sectional area of the soil element (i.e. A = ΔX x ΔY),
E: modulus of elasticity of the soil element.
Consolidation Settlement Analysis
The program estimates the consolidation settlement of each soil element based on Terzaghi 1-D consolidation theory.
Ground Settlement
Settlement at the ground surface for each soil element is calculated based on a summation of settlement (ΔS = ΔSe + ΔSc) of all soil elements exactly below that soil element (i.e. all soil elements sharing the same X and Y, but different Z).